Flow Matching and Diffusion Models
Introduction
生成对象（Object）：对图像，视频，蛋白质等数据类型可视为向量，即
生成（Generation）：从数据分布中采样，
数据集（Dataset）：服从数据分布的有限样本，
条件生成（Conditional Generation）：从条件分布中采样，
目标：训练生成模型，将初始分布（）的样本转化为数据分布样本
Flow and Diffusion Models
通过模拟常微分方程（Ordinary Differential Equations, ODEs）和随机微分方程（Stochastic Differential Equations, SDEs）可以实现从初始分布到数据分布的转换，分别对应Flow Model和Diffusion Model
Flow Models
Flow Model可以由ODE来描述，即
其中向量场 为神经网络，为参数。描述了由引起的Flow，为ODE方程解（Trajectory）的集合
通过使用Euler算法，可以模拟ODE计算出Flow，实现从Flow Model中采样
Diffusion Models
Diffusion Model可以由SDEs描述，如下所示（由于其随机性SDEs不使用微分表示形式）
其中 为diffusion系数，为随机过程 布朗运动（Brownian motion）
可以看出Diffusion Model是Flow Model的一个拓展，当时即为Flow Model
同样的，可以使用以下算法实现从Diffusion Model中采样
Training Target and Train Loss
对于Flow Model和Diffusion Model
训练可以通过最小化以下损失实现
为网络模型，为目标向量场，其实现将初始数据分布转化为目标数据分布，为了实现计算 或者间接计算 需要构建。
Probability Path
Probability Path是从初始分布到目标数据分布的渐进插值（gradual interpolation），分为条件概率路径（conditional probability path）和边缘概率路径（marginal probability path），分别为 和 ，其中：
可由以下公式获得
Training Target for Flow Model
对于，记为条件概率路径 对应的条件向量场，即
则可定义为
且满足：
其中。
这可以由Continuity Equation 证明
Continuity Equation
对于向量场 且 ，有 在 成立有且仅有
其中，
Training Target for Diffusion Model
同样的，对于Diffusion Model，可以构建如下所示，满足 ，即
并且将 替换为 时仍然成立
其中， 称为marginal score function， 称为conditional score function，二者满足
这可以由Fokker-Planck Equation证明
Fokker-Planck Equation
对于 描述的SDE， 成立，当且仅当
其中，
Remark Langevin dynamics
当时，即概率路径为静态时，有
此时 ，即Langevin dynamics
Gaussian probability path
设噪声调度为单调连续可微函数且，定义Gaussian conditional probability path为
其满足
则从其marginal path中采样可以通过以下方法得到
基于Gaussian probability path的conditional Gaussian vector field可以计算得到
其中，
同样的可以得到其marginal score function为
Flow Matching
对于Flow Model，定义flow matching loss为
定义conditional flow matching loss为
其中可以人为构造获得（例如Gaussian probability path）
可以证明，
即
因此优化即优化，而对于，只需构造probability path即可，至此可以得到训练Flow Model的算法，整个流程即称为Flow Matching
Flow Matching for Gaussian Conditional Probability Paths
对于Gaussian Probability Path，有
特别的，对于，，有
称之为(Gaussian) CondOT probability path，训练过程如下所示
Score Matching
对于Diffusion Models，由于 难以得到，因此使用score network 对score function进行拟合，同样的，存在score matching loss和conditional score matching loss如下
同样的，虽然未知，但可以人工构造，且存在
因此，优化即可，此时采样过程如下所示
其中，尽管理论上对任意均可实现采样，但由于存在对随机微分方程模拟不精确导致的精度误差，以及训练误差，因此存在一个最优的。同时观察采样过程可以发现模拟该SDE还需学习，但其实通常可以使用一个两输出的网络同时处理和，并且对于特定的概率路径，两者可以相互转化。
Denoising Diffusion Models: Score Matching for Gaussian Probability Paths
对于Gaussian Probability Paths，有
则
由于在趋近于0时loss趋近于无穷大，因此通常舍弃常数项，并用以下方法reparameterize 为（噪声预测网络）得到DDPM损失函数
其训练过程如下所示
此外，对于Gaussian Probability Paths，vector field和score可以相互转化，即
proof
和 也可以相互转化，有
因此对于Gaussian probability paths来说，只需训练或 即可，且使用flow matching或者使用score matching的方法均可
最后，对于训练好的 从SDE中采样过程如下
Summary
总的来说，Flow Matching比Score Matching更简洁并且Flow Matching更具有拓展性，可以实现从一个任意初始分布得到任意分布，但是denoising diffusion models只适用于Gaussian initial distributions and Gaussian probability path。Flow Matching类似于Stochastic Interpolants。
Conditional (Guided) Generation
在给定条件下进行生成（generate an object conditioned on some additional information），称之为conditional generation，为了和conditional vector field区分多称为guided generation
用数学语言描述即，对于，对中采样，因此模型包含条件向量场，模型架构如下所示
对于给定的，采样过程可以描述为
上述在时即为guided flow model
Guided Models
Guided Flow Models的训练损失（优化目标，或者说guided conditional flow matching objective）很容的得到，如下所示
同样的，对于Guided Diffusion Models，有guided conditional score matching objective如下
虽然理论上上述以及足够生成标签对应样本，但是实际上生成效果并不十分fit ，以及，无法控制生成内容对label的fit程度。一种解决方法是人为加强的作用，比较先进的技术是Classifier-Free Guidance。
Classifier-Free Guidance
对于Flow Models，以Gaussian probability paths为例
其中
又
则
可以看出，guided vector field是由unguided vector field和guided score相加得到，一种很自然的想法是对guided score进行加权，得到
其中guided score可以看作是噪声类别分类器，早期的工作确实使用这样的方法实现，但是进一步对guided score进行分析得到如下：
即由unguided vector field和guided vector field加权得到，并且，通过构造其对应概率为人为设计的超参数，从而实现使用代替，具体可公式化描述为
对于Diffusion Models，同样可改写如下
training objective如下
训练时，我们通常也可同时优化和，对应的，有
采样时，有
Network architectures
网络模型的设计随建模数据的复杂程度各有差别，但都需满足
U-Nets
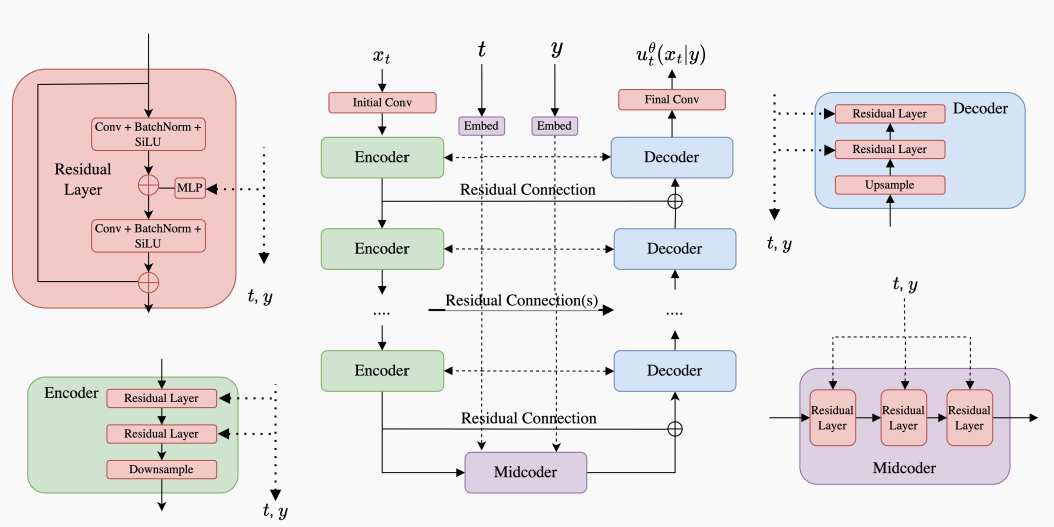
Diffusion Transformers
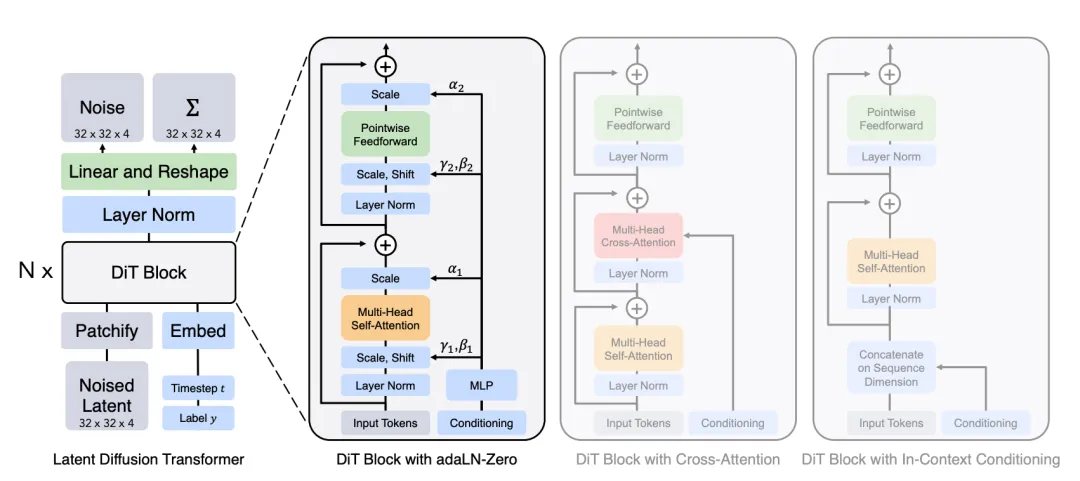
References
[1] Peter Holderrieth and Ezra Erives.An Introduction to Flow Matching and Diffusion Models[EB/OL].https://arxiv.org/abs/2506.02070,2025.